Yesterday's lesson was interesting and made simple with a slight flavour of primary school math. Reading this might provide some answers to what's going through our minds now.
A Brief History of Singapore Math by a source from the US
A relatively small and densely populated island, Singapore’s only natural resource is their people. The country has chosen to focus on building strong Singaporean citizens beginning with their earliest education.
The mathematics curriculum was developed with this goal in mind. The first primary mathematics curriculum was developed in 1981 by the Curriculum Development Institute of Singapore. In Singapore, it is simply referred to as “maths”.
The term “Singapore Math” refers to the Marshall Cavendish Primary Mathematics series of materials used in the U.S. and several other countries.
The 1981 curriculum focused on basic content. This curriculum was revised in 1992 to make it a problem solving curriculum. The Primary Mathematics (2nd Edition) was based on the 1992 curriculum.
The Primary Mathematics (3rd Edition) series was based on a reduced syllabus in 1994. In 1999, Singapore’s Ministry of Education decided to reduce the content in the curriculum up to 30% for most subjects.
In 1998, the first books were imported from Singapore for use in this country (Primary Mathematics 3rd Edition). These books were written in British English and contained Singaporean money and only metric measurement. The U.S. Edition was created in 2001 and included American measurement and money.
The most recent series published in the United States is the Primary Mathematics Standards Edition. This series was designed to meet all state standards in California; a state that has written standards based on the National Council of Teachers of Mathematics (NCTM) Focal Points.
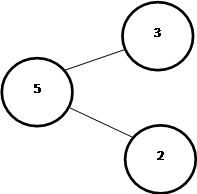
Number bonds is a concept used in Singapore Math. It is a visual image that can be used to show the relationship between addition and subtraction. Number bonds consists of a minimum of three circles connected by lines. The “whole” is written in the first circle and its “parts” are written in the adjoining circles. The "parts" when added together will then equal the "whole"
The following number bond can be used to represent four number sentences.
3 + 2 = 5, 2 + 3 = 5, 5 − 3 = 2, 5 − 2 = 3
3 + 2 = 5, 2 + 3 = 5, 5 − 3 = 2, 5 − 2 = 3
Numbers To 10: Making number bonds with cubes
The video shows how number bonds can be used to "split" numbers.
The video shows how number bonds can be used to "split" numbers.
What makes 10? Basic number facts to 10 using the tens frame
No comments:
Post a Comment